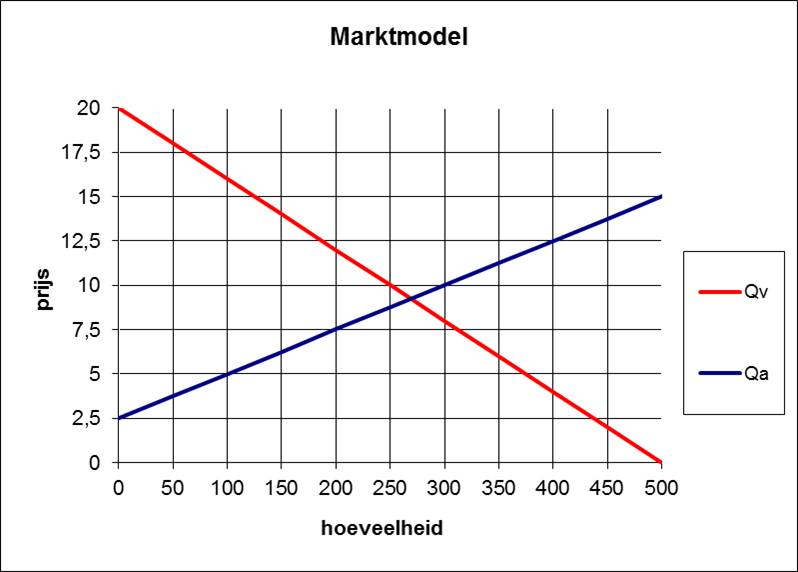
Een markt van volkomen concurrentie kan in de uitgangssituatie met de volgende vraag- en aanbodvergelijkingen worden beschreven:

Qv = -25P + 500
Qa = 40P – 100		 waarbij:
P in euro’s per stuk
Q in mln stuks
a

Teken de vraag- en aanbodvergelijking in onderstaande figuur.
 

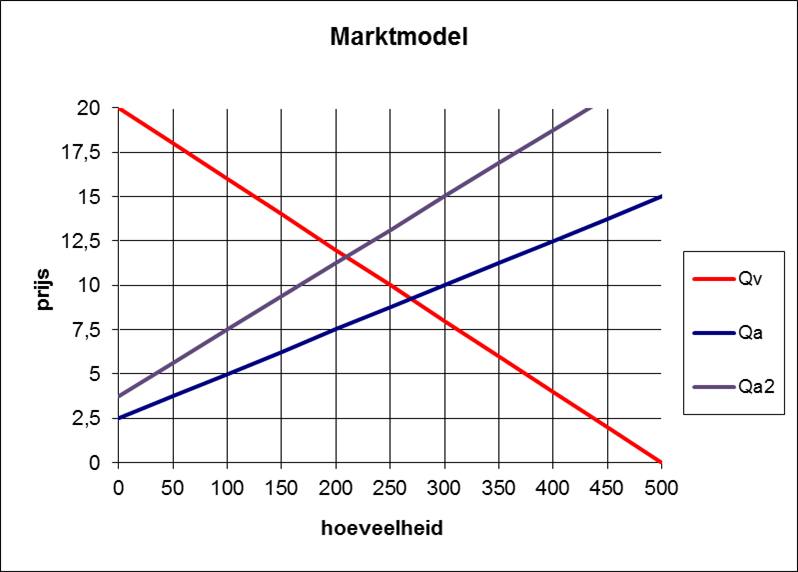
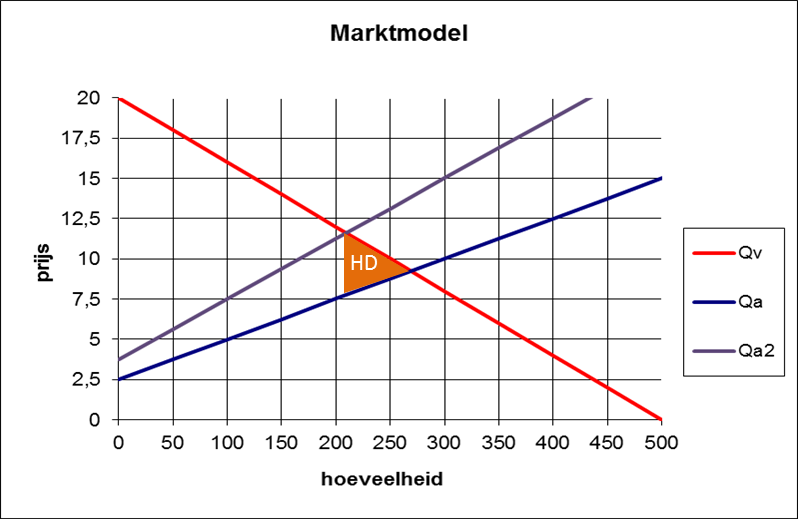
De overheid gaat over tot het belasten van dit product met een heffing van 50%.

b

Arceer in de figuur het totale welvaartsverlies dat door de heffing ontstaat.
Bereken en teken daarvoor eerst de nieuwe vergelijking(en).

Een producent op deze markt, die streeft naar maximale winst, heeft een productiecapaciteit van 12.000 stuks en de volgende kostenfunctie:
TK = 0,4Q2 + 1.750 (waarbij Q in 1.000 stuks)

c

Bereken bij welke productie-omvang deze producent zijn maximale totale winst zal behalen.

a Bereken eerste de nulpunten van de vraaglijn:

  • Als P = 0, dan is Qv = 500
  • Als Qv = 0, dan is P = 20

Bereken dan het beginpunt van de aanbodlijn:

  • Als Qa=0, dan is P = 2,5

En kies dan een tweede punt op de aanbodlijn. Bijvoorbeeld:

  • Als P= 12,5, dan is Qa = 400
b

Stap 1 – nieuwe aanbodvergelijking

Qa = 40P – 100
-40P = -Q – 100
P = 0,025Q + 2,5

door de heffing wil de producent voortaan 50% hogere prijs, zodat zijn eigen opbrengst hetzelfde blijft:
P = (0,025Q + 2,5) × 1,50
P = 0,0375Q + 3,75

-0,0375Q = -P + 3,75
Qa = 26,67P – 100

Stap 2 – intekenen nieuwe aanbodvergelijking

Stap 3 – surplus
Na de instelling van de heffing onstaat een Harberger Driehoek (HD) die het welvaartsverlies laat zien.

Harberger driehoek bij heffing
c

Maximale totale winst wordt behaald bij de productieomvang waar MO=MK

Marginale opbrengst
Er is sprake van volkomen concurrentie. Dus de producent heeft geen individuele invloed op de prijs.
Door de heffing ontstaat een nieuwe evenwichtsprijs van:

Qa = Qv
26,67P – 100 = -25P + 500
51,67P = 600
P = 11,62

Deze € 11,62 is echter de consumentenprijs, inclusief 50% heffing.
De consumentenprijs is dus 150% van de producentenprijs.
De producent krijgt dus uiteindelijk (maar) € 7,75
MO = 7,75

Marginale kosten
Er is hier geen sprake van proportioneel variabele kosten.
Om de MK te bepalen, moeten we dus de TK-functie differentiëren:
TK = 0,4Q2 + 1.750
MK = 0,8Q
 
Maximale winst bij MO=MK
7,75 = 0,8Q
Q= 9,7
 
Het bedrijf moet dus 9.700 producten gaan maken
print