Van een bepaald landbouwproduct in gegeven dat de vraagfunctie luidt:
| Qv = -20P + 10.000 | waarbij geldt: P = prijs in centen per kilogram Q = hoeveelheid in 1.000 kg. per week |
In week 1 bedraagt het aanbod van de groente:
Qa = 4.000
| a |
Teken de marktsituatie van week 1 |
| b |
Bereken de evenwichtsprijs in week 1 |
Het komt regelmatig voor dat de prijs van deze groente, bij vrije marktwerking, onacceptabel laag zou worden. De overheid heeft daarom een fonds in het leven geroepen om de boeren een minimale opbrengst van € 2 per kilo te garanderen.
Om de kosten van het veilingfonds te drukken, moeten de boeren zélf 1% van hun omzet in het fonds storten als de marktprijs boven de minimumprijs ligt.
| c |
Bereken hoeveel de boeren in week 1 moeten storten in het garantiefonds. |
In week 2 neemt, door goede weersomstandigheden het aanbod toe:
Qa = 6.500
| d |
Bereken het aanbodoverschot dat ontstaat door dit grote aanbod. |
| e |
Hoeveel bedragen de kosten voor het garantiefonds in week 2? |
| a |
Qv = -20P + 10.000
Qv = -20 × 0 + 10.000 Qv = 10.000 Als Qv = 0 : Qv = -20P + 10.000 |
| b |
Qv = Qa Zodat de evenwichtsprijs € 3 per kilo bedraagt. |
| c |
Bij een prijs van € 3 per kilo en een afzet van 4.000 ton, bedraagt de omzet: 1% van deze omzet moeten zij afdragen, dus: € 120.000 |
| d |
De vraag zal bij p = 200: Het aanbod bedraagt: Er is dus een overschot van 500 (× 1.000 kilo). Dus 500.000 kilo. |
| e |
Dit aanbodoverschot van 500.000 kg. zal door het fonds moeten worden opgekocht tegen een prijs van € 2 (garantieprijs). |
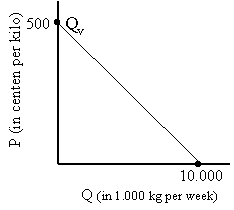Als P = 0 :
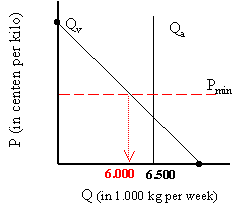We kunnen uitrekenen dat de evenwichtsprijs (€ 1,75) ónder de minimumprijs zou komen.