In onderstaande opgaven worden steeds rentepercentages voor spaarrekeningen genoemd die lange tijd heel normaal waren in Nederland, maar wellicht op dit moment wat abnormaal lijken.
Met de huidige rentepercentages van bijna o% zou je fouten in de berekening niet meer kunnen herkennen.
Vraag 1
Onderstaande tabel schets een aantal korte spaartransacties.
Omdat er maximaal sprake is van één jaar sparen, is er sprake van enkelvoudige rente.
| Storting | Rente-percentage op jaarbasis | Looptijd | |
|---|---|---|---|
| A | € 1.500 | 3,4% | 1 jaar |
| B | € 250.000 | 1,75% | 30 weken |
| C | € 750 | 2,8% | 8 maanden |
| D | € 500 | 1,4% | 1 kwartaal |
| E | € 10.000 | 3,1% | ½ jaar |
| a |
Bereken hoeveel rente elke storting gedurende de genoemde looptijd oplevert. |
De inflatie is Nederland is gemiddeld genomen zo’n 1,8%.
| b |
In welke regel(s) neemt de koopkracht voor de spaarder AF doordat het geld niet direct wordt uitgegeven? Verklaar je antwoord. |
| c |
Bereken hoeveel procent de koopkracht van de spaarder in regel A toeneemt als de inflatie 1,8% is gedurende dat jaar. |
In 2020 krijgt een spaarder nog 0,01% rente over spaargeld, terwijl de inflatie 2,1% is.
Spaarders leveren dus koopkracht in. Zeker als ze ook nog belasting moeten betalen over hun spaargeld. Desondanks zijn Nederlanders méér gaan sparen.
| d |
Leg uit waarom Nederlanders méér zijn gaan sparen, ondanks de extreem lage rente. Verklaar je antwoord met het gebruik van de spaarmotieven. |
Omdat sparen niet veel oplevert, gaan steeds meer mensen hun geld beleggen in aandelen.
Stel dat twee beleggers € 10.000 stoppen in aandelen waarvan de koers mee verandert met de AEX.op
Beide beleggers beleggen precies 1 jaar en ontvangen gedurende dat jaar € 130 dividend.
| e |
Bereken voor beide beleggers het rendement van hun belegging. |
| f |
Moet belegger B zijn aandelen langer vast houden of snel verkopen? Verklaar je antwoord. |
Vraag 2
Onderstaande tabel beschrijft enkele spaartransacties over meerdere jaren, waardoor sprake is van samengestelde rente.
We gaan er voor het gemak vanuit dat alle bedragen op 1 januari gestort worden en de rente jaarlijks uitgekeerd wordt.
| Storting | Rente-percentage op jaarbasis | Looptijd | |
|---|---|---|---|
| A | € 1.200 | 2,4% | 5 jaar |
| B | € 150.000 | 0,75% | 10 jaar |
| C | € 7.500 | 3,8% | 6 jaar |
| D | € 50.000 | 1,4% | 15 jaar |
| a |
Bereken het saldo op de spaarrekening na de genoemde looptijd. |
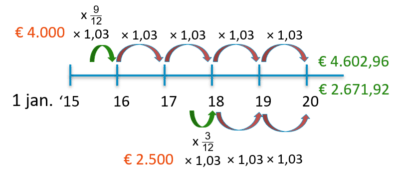
Karim opent op 1 april 2015 een spaarrekening tegen een rentepercentage van 3%. Hij stort direct € 4.000.
Op 1 oktober 2017 stort hij nog eens € 2.500.
| b |
Wat is het saldo van de spaarrekening op 31 maart 2020? |
| c |
Hoeveel geld krijgt hij als hij op 31 maart 2020 de rekening opheft. |
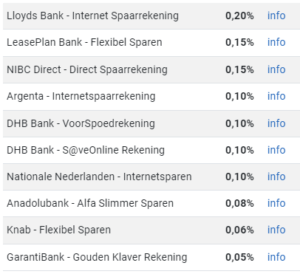
Even terug naar de werkelijkheid levert een zoektocht naar de verschillende rentepercentages die banken bieden op spaargeld in mei 2020 het volgende overzicht:
Dit zijn de 10 spaarrekeningen die de hoogste rente opleveren.
| d |
Waarom biedt de ene ‘bank’ een hogere rente dan een andere ‘bank’? Verklaar je antwoord. |
| e |
Sommige aanbieders van spaarrekeningen zijn niet gevestigd in Nederland. Noem twee mogelijke nadelen als iemand hiervoor kiest. |
| f |
Hoeveel procent levert de hoogst renderende spaarrekening meer op dan de nr. 10 uit het overzicht? |
Vraag 3
Het bedrijf Appel plaatst een obligatielening gesplitst in obligatie’s met een nominale waarde van € 100, een looptijd van 1 jaar en een jaarlijkse couponrente van 6,5%. Het bedrijf hoopt op die manier € 1 mln. op te halen.
Jenny koopt op 1 januari één obligatie voor € 105.
| a |
Verklaar waarom het bedrijf de lening van € 1 mln. opknipt in stukjes van € 100. |
| b |
Hoeveel rente zal Jenny ontvangen op haar obligatie? |
| c |
Bereken het rendement dat Jenny behaalt met haar belegging. |
Het bedrijf Pear plaatst op hetzelfde moment een obligatielening voor 10 jaar.
De lening wordt in obligatie’s met een nominale waarde van € 100 verdeeld. De jaarlijkse couponrente is 8%.
In totaal moet de lening € 1 mln. opleveren.
Jenny koopt ook van dit bedrijf 1 obligatie. Hiervoor betaalt zij € 102,50.
| d |
Noem twee (mogelijke) redenen waarom de rente op deze obligatielening hoger is dan bij de obligatielening van Appel. Verklaar je antwoord. |
| e |
Hoeveel rente zal Jenny voor deze obligatie gedurende de gehele looptijd ontvangen? |
Na twee jaar gaat de spaarrente bij de banken eindelijk weer omhoog.
Jenny besluit haar obligatie van Pear te verkopen en het geld weer op een spaarrekening te zetten.
| f |
Leg uit waarom Jenny waarschijnlijk verlies zal maken op de koers van de obligatie. |