Om in grafieken waarin waarden per product staan tóch totaalbedragen aan te kunnen geven, moet je gebieden arceren.
In het examenprogramma vwo staan twee arceringsvormen: rechthoeken en driehoeken.
Aan de hand van een aantal veelvoorkomende situaties zullen we de regels van het arceren nader bekijken.
In ieder geval geldt altijd:
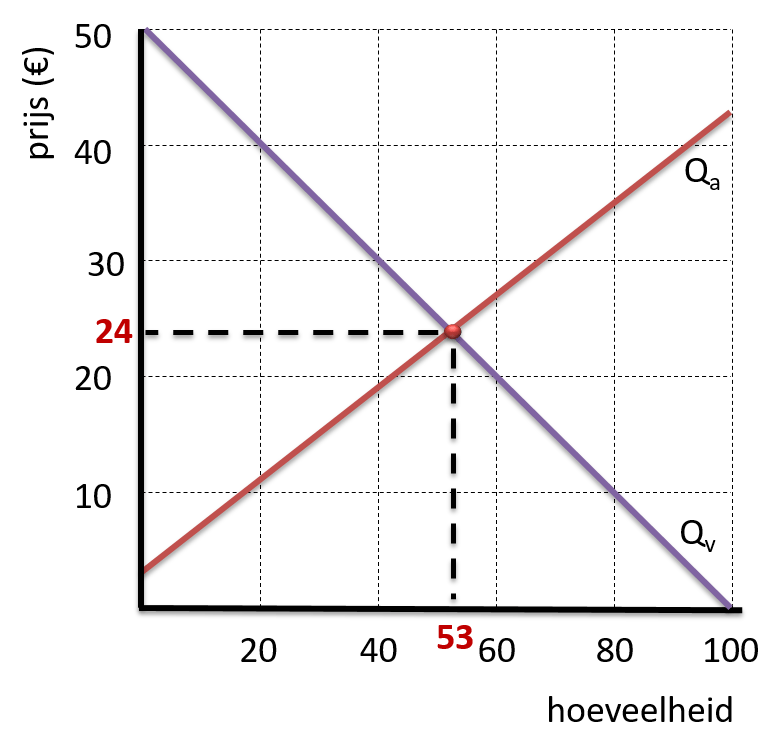
Omzet in marktmodel
Formule omzet: TO = P × Q
In dit model zoeken we de benodigde waarden bij het marktevenwicht:
- een prijs van € 24
- en een hoeveelheid van 53 stuks.
De marktomzet bedraagt dus:
€ 24 × 53 stuks = € 1.272
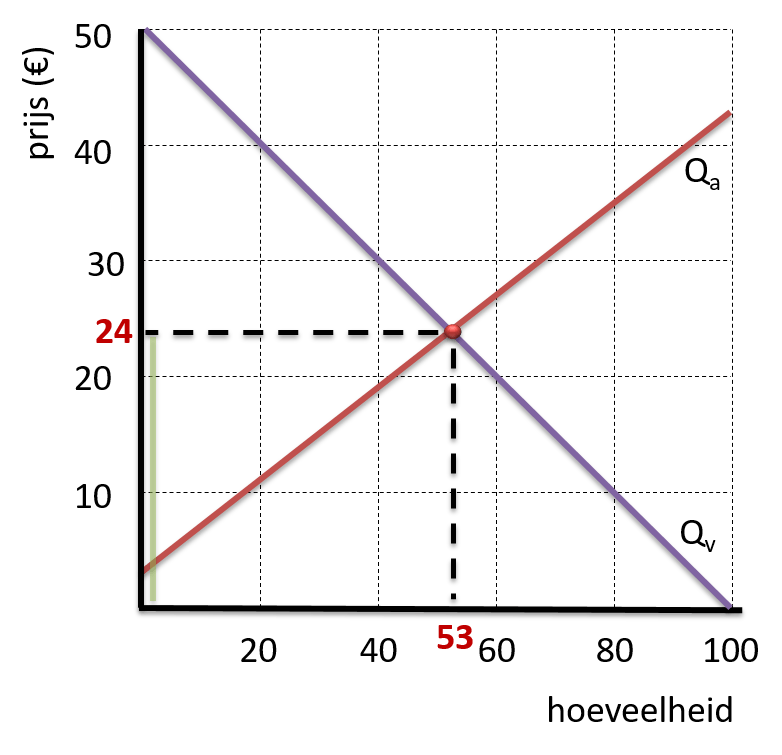
De prijs van het eerste product kunnen we ook aangeven met een groen balkje.
Dat product levert € 24 omzet op.
Zo’n staafje van € 24 kunnen we voor alle producten die verkocht worden in de grafiek zetten: er komen dan 53 staafjes van € 24 in de grafiek.
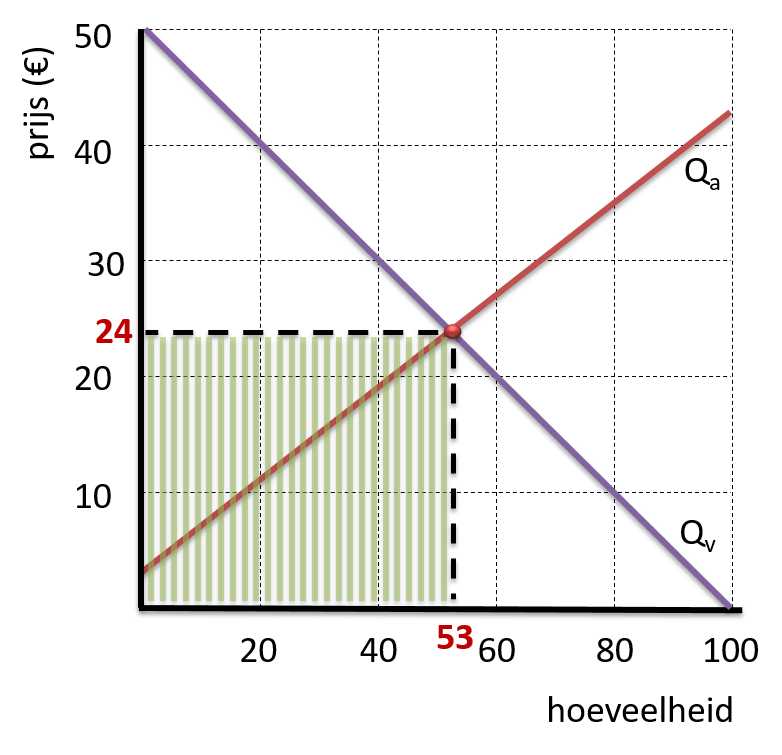
Omzet = prijs × hoeveelheid
Omzet = € 24 × 53 stuks = € 1.272
Grafisch gezien ontstaat zo een rechthoek.
De oppervlakte van deze rechthoek kunnen we uitrekenen door:
breedte × lengte = opppervlakte
53 staafjes × € 24 = oppervlakte / omzet.
Het groen gearceerde gebied heeft dus een oppervlakte van € 1.272 ⇒ de marktomzet.
Wanneer de staafjes per product allemaal even lang zijn, ontstaat bij het arceren een rechthoek.
Dan geldt:
Oppervlakte rechthoek = Lengte × Breedte
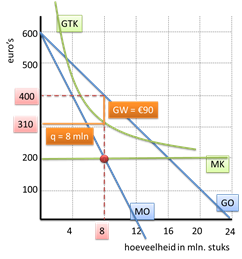
Maximale totale winst bij een monopolist
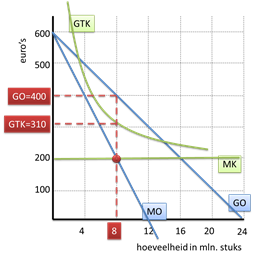
De monopolist haalt maximale totale winst bij de productie-omvang waar MO=MK.
Om de totale winst uit te rekenen hebben we nodig:
- de winst per product
(in dit geval te vinden door het verschil tussen GO en GTK) - het aantal producten
In dit geval zal hij dus kiezen voor een productie-omvang van 8 mln. stuks.
Bij die productieomvang kunnen we aflezen:
via de GO-lijn dat de prijs (GO) € 400 is
en via de GTK-lijn dat de gemiddelde totale kosten € 310 bedragen.
Dat wil dus zeggen dat de monopolist:
LENGTE = 8 mln. stuks produceert
BREEDTE = € 90 winst per product (GW) behaalt.
Totale winst = winst per product × hoeveelheid
Oppervlakte = breedte × lengte
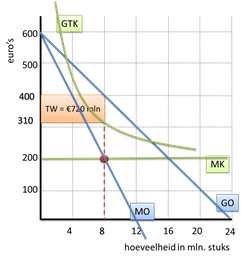
Het gearceerde gebied heeft dus een oppervlakte van € 720 mln. – de (maximale) totale winst.
Er staan dus 8 miljoen staafjes van € 90 winst naast elkaar.
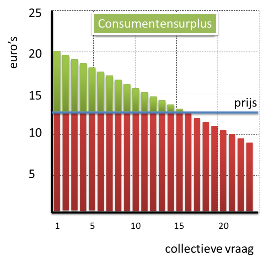
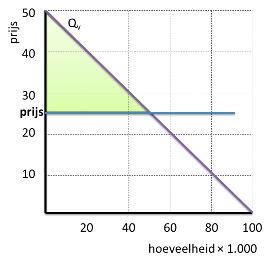
Consumentensurplus
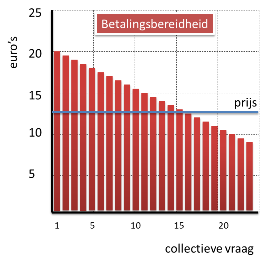
De vraaglijn geeft de maximale betalingsbereidheid van de consumenten weer.
Voor de uitleg van het arceren weergegeven met staafjes in plaats van een lijn.
Het consumentensurplus geeft aan dat een consument bereid is om méér te betalen dan de marktprijs.
Het surplus is niet voor elke consument hetzelfde. Iemand met een hoge betalingsbereidheid heeft een groter surplus dan iemand met een lagere betalingsbereidheid.
Wanneer we het totale surplus gaan arceren, komen er dus staafjes van verschillende lengte; er ontstaat een driehoek.
Werken we met een lijn in plaats van losse staafjes, dan arceren we dus de driehoek die zo ontstaat.
Ook die oppervlakte kunnen we uitrekenen:
Oppervlakte driehoek = ½ × basis × hoogte
In dit geval:
Surplus = ½ × (€ 50 – € 25) × 50.000 = € 625.000