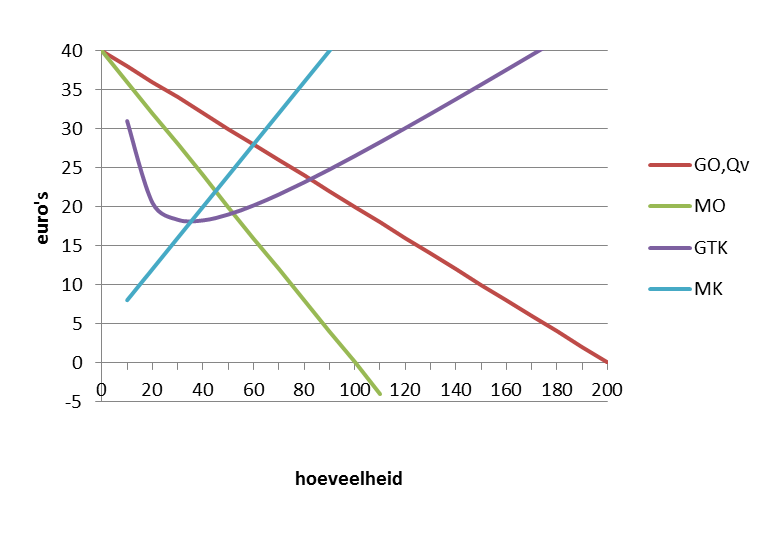
Onderstaande grafiek toont het kosten en opbrengstenverloop van een monopolist.

monpolist2_01

Qv = -5P + 200
TK = 0,2Q2 + 4Q + 250
(bedragen in euro’s en hoeveelheden in stuks per dag)

a

Herleid met behulp van bovenstaande gegevens de MO-functie.
b

Herleid met behulp van bovenstaande gegevens de MK-functie.
c

Bereken hoeveel producten deze monopolist dagelijks zal aanbieden indien hij streeft naar maximale totale winst.
(Berekenen, dus geen gegevens aflezen!)
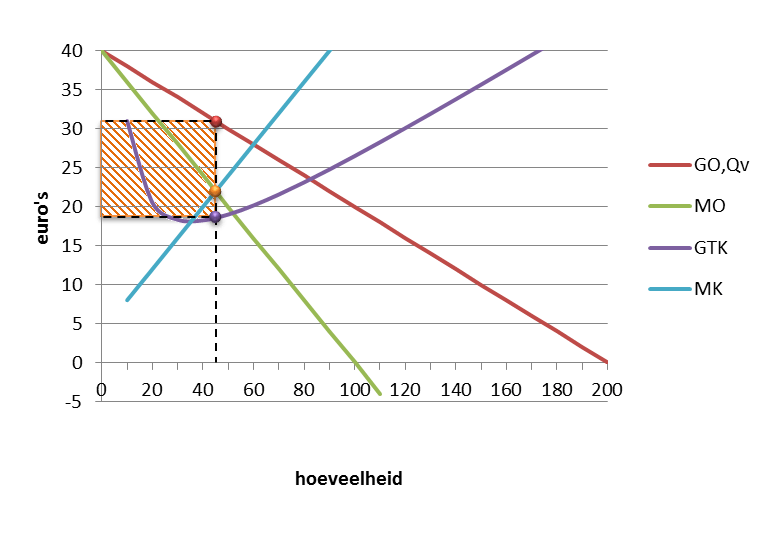
d

Arceer in de grafiek de maximale totale winst die deze producent dagelijks behaalt. 
e

Omdat het bedrijf in liquiditeitsproblemen verkeert, besluit de directie om voortaan te streven naar maximale totale omzet.
Kan het bedrijf in die situatie nog winst behalen? Verklaar je antwoord met een berekening.

a

MO = verandering van de totale opbrengst als er één product méér gemaakt wordt.
Dus: de stijging van TO, dus de afgeleide van TO (differentiëren).
TO = P × Q

Stap 1: wissel P en Q van plek (zodat de P voor het =teken staat):
Qv = -5P + 200
P = -0,2Q + 40

Stap 2: TO = P × Q:
TO = (-0,2Q = 40) ×Q
TO = -0,2Q2 + 40Q

Stap 3: TO differentiëren = MO
MO = -0,4Q + 40
b

MK = verandering van de totale kosten als er één product méér gemaakt wordt.
Dus: de stijging van TK, dus de afgeleide van TK (differentiëren).

TK = 0,2Q2 + 4Q + 250

MK = 0,4Q + 4
c

Een monopolist behaalt maximale totale winst bij de productieomvang waar geldt: MO = MK

-0,4Q + 40 = 0,4Q + 4
-0,8Q = -36
Q = 45

Maximale winst wordt behaald bij een productieomvang van 45 stuks per dag.
d

Oranje bolletje: het punt waar MO = MK (om de productieomvang te kunnen vinden)

Rode bolletje: de prijs (GO) die geldt bij de gekozen productieomvang.
Paarse bolletje: de kosten (GTK) die gelden bij de gekozen productieomvang.

Het gearceerde gebied ontstaat doordat je (GO-GTK) × Q doet.
En lengt × breedte is de oppervlakte van een rechthoek.

monpolist2_02
e

Maximale omzet wordt door een monopolist behaald bij een productieomvang waar geldt: MO = 0

MO = -0,4Q + 40 = 0
Q = 100

In dat geval wordt de prijs: P = -0,2Q + 40 = € 20

TK = 0,2Q2 + 4Q + 250
GTK = 0,2Q + 4 + (250:Q) = € 26,50

De kosten liggen dus hoger dan de opbrengsten. Winst behalen is dus niet mogelijk bij deze doelstelling.
print