In de uitgangssituatie kan de economie van land X beschreven worden aan de hand van onderstaand model.
Land X heeft geen relaties met het buitenland.

(1) C = 3/4 (Y – B) + 20
(2) B = 1/3 Y
(3) I = 45
(4) O = 85
(5) EV = C + I + O
(6) Y = EV

Wanneer we dit model snel oplossen, komt er een evenwichtsinkomen uit van 300.

Y = 0,75 (Y – 0,33Y) + 20 + 45 + 85
Y = 0,5Y + 150
0,5Y = 150
Ȳ = 300

Grafisch

Een model kan ook grafisch worden weergegeven / opgelost.

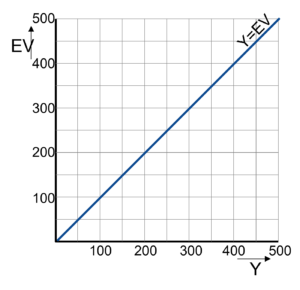
Het begint met een basisgrafiek, waarin horizontaal het nationaal inkomen (Y) en verticaal de omvang van de bestedingen (EV) bij dat inkomen staat.
We tekenen direct een evenwichtslijn in de grafiek: een lijn die aangeeft dat EV en Y aan elkaar gelijk zijn.
Dankzij een gelijke assenverdeling, wordt dat automatisch een 45°-lijn.

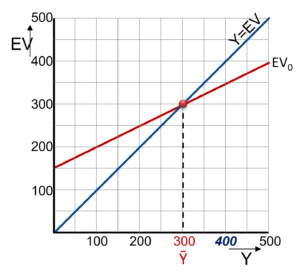
Opnemen van de EV-lijn

Het model beschrijft dat de EV afhankelijk is van de hoogte van Y.
Namelijk: EV = C + I + O

Wanneer we dat verder oplossen:
EV = C + I + O
EV = 0,75 (Y – 0,33Y) + 20 + 45 + 85
EV = 0,5Y + 150

Dat wil zeggen dat:

  • Bij Y = 0; dan EV = 150
    EV = 0,5 × 0 + 150

  • Bij Y = 500; dan EV = 400
    EV = 0,5 × 500 + 150 = 400

Wanneer we de EV-lijn opnemen in de basisgrafiek, kunnen we dankzij de evenwichtslijn snel het evenwichtsinkomen vinden. Namelijk Ȳ = 300.

Bestedingsimpuls en multiplier

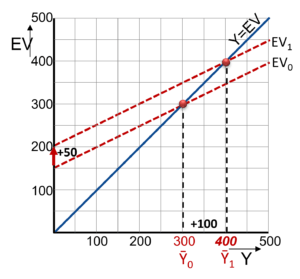In de grafiek zien we dat een autonome besteding met 50 is toegenomen; de EV-lijn is evenwijdig met 50 naar boven verschoven.

Met behulp van de evenwichtslijn zien we dat het evenwichtsinkomen naar Ȳ = 400 verschuift. Een toename van 100.
Dat wil dus zeggen: een multiplier van 2.

Grafisch gezien wordt de multiplier groter als de helling van de EV-lijn groter is.
Die helling wordt bepaald door de marginale quotes (c, b) in met model, want die geven aan hoe groot het spaarlek en het belastinglek zijn.

  • Een hoge marginale consumptiequote (c) betekent een klein spaarlek. Dus een grotere multiplier (en een grotere helling van de EV-lijn).

  • Een hogere marginale belastingquote (b) betekent een groter belastinglek, dus een kleinere multiplier en een vlakker lopende EV-lijn.

De arbeidsmarkt in het grafische model

Het model kunnen we weer uitbreiden met een arbeidsmarkt.
waarbij Y in miljarden euro’s en A in miljoen arbeidsjaren

Av =
apt = 80.000
Aa = 5
U = Aa – Av

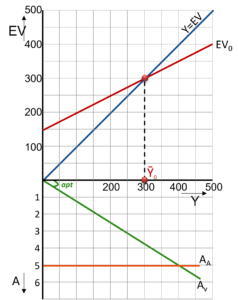
Onder de eerste grafiek zetten we nu een as die de hoeveelheid arbeid afzet tegenover het nationaal inkomen.

De groene Av-lijn laat zien hoeveel arbeid er gevraagd wordt bij een bepaald inkomen (productie). De helling van deze lijn hangt af van de hoogte van de arbeidsproductiviteit. Hoe hoger de arbeidsproductiviteit, hoe minder arbeidskrachten er voor een bepaalde productie nodig zijn, hoe vlakker de lijn verloopt.

De oranje Aa-lijn laat de omvang van de beroepsbevolking op een bepaald moment zien. Meestal beschouwen we dat als een exogene grootheid, omdat het om een korte termijn-model gaat.

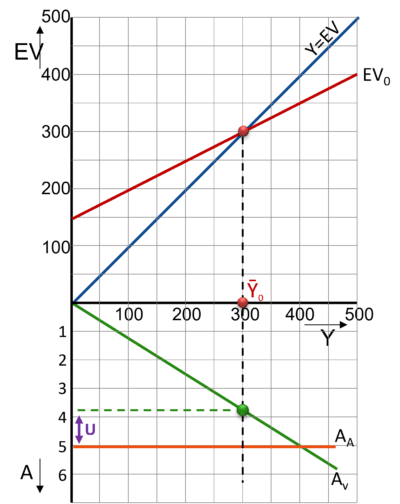In het bovenste deel van de grafiek kunnen we het evenwichtsinkomen aflezen.
In dit geval is dat 300 mld. euro.

Wanneer we nu de lijn doorstippelen naar beneden, kunnen we ook de arbeidsvraag (en arbeidsaanbod) aflezen.
De arbeidsvraag bedraagt 3,75 mln. arbeidsjaren.
Het arbeidsaanbod is in het model altijd 5 mln. arbeidsjaren. 
De werkloosheid (U) bedraagt dus 1,25 mln. arbeidsjaren.

Met deze grafiek kunnen we snel zien wat er gebeurt als de bestedingen veranderen, de arbeidsproductiviteit verandert, enz..
Bedenk daarbij welke lijn verandert. Of de lijn evenwijdig verschuift of de helling verandert. En lees daarna het resultaat van de verandering af.

print