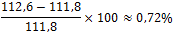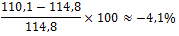Om de ontwikkeling van verschillende grootheden, zoals prijzen, inkomen of productievolume, goed te kunnen vergelijken wordt vaak gebruik gemaakt van indexcijfers.
Elk examen bevat sommen met indexcijfers. Zorg er dus voor dat je het onderstaande goed beheerst.
Indexcijfers
Een indexcijfer is een verhoudingsgetal waarmee de grootte van een bepaald verschijnsel wordt uitgedrukt ten opzichte van datzelfde verschijnsel in een andere periode.
De periode waarmee we alle andere periodes vergelijken noemen we het basisjaar.
Dit basisjaar krijgt het indexcijfer 100 (wordt op 100% gesteld).
Daardoor geldt dat:
- een indexcijfer boven de 100 duidelijk maakt dat er een procentuele stijging is ten opzichte van het basisjaar.
- een indexcijfer onder de 100 duidelijk maakt dat er een procentuele daling is ten opzichte van het basisjaar.
Voorbeeld 1
In 2014 (het basisjaar) had Dhr. Wolters een inkomen van € 50.000. Een jaar later bedroeg zijn inkomen € 58.000, terwijl in 2016 zijn inkomen € 61.000 bedroeg.
| jaar | waarde | berekening | indexcijfer |
| 2014 | 50.000 | De € 50.000 uit het basisjaar wordt op indexcijfer 100 gesteld. | 100 |
| 2015 | 58.000 |
Zijn inkomen is nu € 58.000. In verhouding tot zijn inkomen in het basisjaar is dat Het indexcijfer 116 wil zeggen dat het inkomen in 2015 met 16% is gestegen ten opzichte van het basisjaar 2014. |
116 |
| 2016 | 61.000 |
Zijn inkomen bedraagt € 61.000. Indexcijfer 2016= Dat wil zeggen dat het inkomen in 2016 met 22% gestegen is ten opzichte van het basisjaar 2014. |
122 |
Voorbeeld 2
We bekijken de ontwikkeling van het nationaal inkomen van een land.
Als basisjaar nemen we het jaar 2013.
| jaar | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| nationaal inkomen (in mld. euro) | 504 | 515 | 554 | 576 | 580 | 591 |
| berekening indexcijfers | 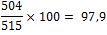 |
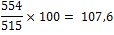 |
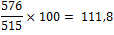 |
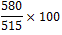 |
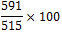 |
|
| nationaal inkomen indexcijfers | 97,9 | 100 | 107,6 | 111,8 | 112,6 | 114,8 |
Procentuele veranderingen
Een procentuele verandering tussen twee indexcijfers reken je op precies dezelfde manier uit als elke andere procentuele verandering
Om een procentuele verandering uit te rekenen maakt het niet uit of het om indexcijfers, euro’s of aantal producten gaat. Je kunt die allemaal op dezelfde manier berekenen. Voor meer hierover kijk op: uitleg over procenten.
| jaar | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| nationaal inkomen indexcijfers | 97,9 | 100 | 107,6 | 111,8 | 112,6 | 114,8 | 110,1 |
Voorbeeld 1
Bereken de procentuele verandering van het nationaal inkomen in 2015 (ten opzichte van 2014).
Voorbeeld 2
Bereken de procentuele verandering van het nationaal inkomen in 2017 (ten opzichte van 2016).
Vooruitgaan en teruggaan in de tijd bij procentuele veranderingen
Als regel geldt:
Voorbeeld 1: vooruit
Op 1 oktober 2013 telt een school 1000 leerlingen. De directie verwacht dat het leerlingenaantal jaarlijks met 2% zal stijgen.
Gevraagd: Bereken het verwachte aantal leerlingen op 1 oktober 2016
Uitwerking:
1000 x 1,02 x 1,02 x 1,02 = 1061,2
Dus: 1061 leerlingen (vergeet niet af te ronden!)
Voorbeeld 2: achteruit
Op 1 oktober 2016 telt een school 900 leerlingen. Dit is het gevolg van een jaarlijkse stijging van het aantal leerlingen met 3%.
Gevraagd: Bereken het aantal leerlingen op 1 oktober 2012
Uitwerking: (dus: 800)
Basisjaar verleggen
Gegevens voor altijd vergelijken met hetzelfde jaar is onzinnig. Soms is het beter om na verloop van tijd je basisjaar opnieuw vast te stellen. Je huidige nationale inkomen uitdrukken in een indexcijfer ten opzichte van het jaar 1990 is nuttiger dan het te blijven vergelijken met het inkomen uit 1800.
In onderstaand voorbeeld gaan we het basisjaar verleggen van 2005 naar 2008, hoewel zo’n korte verschuiving van basisjaar in werkelijkheid niet erg nuttig is.
De waarde van 2008 (112,6) moet nu op 100(%) gesteld worden, terwijl alle andere waarden daarmee vergeleken moeten gaan worden:
| jaar | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| indexcijfer nationaal inkomen(basisjaar 2005) | 97,9 | 100 | 107,6 | 111,8 | 112,6 | 114,8 |
| berekening | 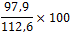 |
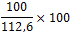 |
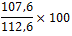 |
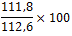 |
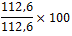 |
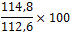 |
| indexcijfer nationaal inkomen(basisjaar 2008) | 86,9 | 88,8 | 95,6 | 99,3 | 100 | 102,0 |
Ook in deze berekening zie je weer dat het niet uitmaakt of er indexcijfers of miljarden euro’s staan. De berekening blijft hetzelfde.