Wanneer de overheid de producenten belast met een heffing (btw, accijns) op hun product, zullen zij alleen bereid zijn hun producten aan te bieden voor een hogere prijs. Zij willen zélf nog steeds hetzelfde bedrag als voorheen over houden. De consument moet dus bovenop dit bedrag ook de heffing betalen om de producenten over te halen dezelfde hoeveelheid aan te bieden.
Door de heffing gaat de aanbodlijn, die de leveringsbereidheid weergeeft, dus omhoog. Om dezelfde hoeveelheid aan te bieden willen de producenten hun oude prijs + de heffing van de consument ontvangen.
Heffing als een vast bedrag per product
Zoals eerder besproken (aanbod, verkoopbereidheid) geeft de aanbodlijn aan welk bedrag producenten minimaal willen ontvangen voordat zij bereid zijn een bepaalde hoeveelheid te leveren.
In deze uitleg bespreken we het effect van een heffing met een vast bedrag per product. In de praktijk gaat het dan meestal om accijns.
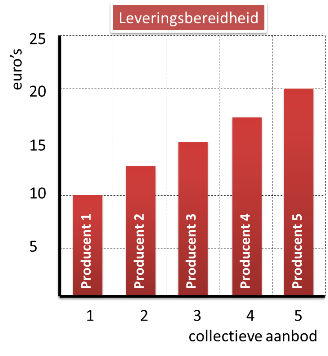
In de eerste grafiek zien we de leveringsbereidheid van 5 producenten. Wanneer de prijs stijgt, zijn steeds meer producenten in staat / bereid om het product te leveren.
Producent 1 wil minimaal € 10
Producent 2 wil minimaal € 12,50
Producent 3 wil minimaal € 15
Producent 4 wil minimaal € 17,50
Producent 5 wil minimaal € 20
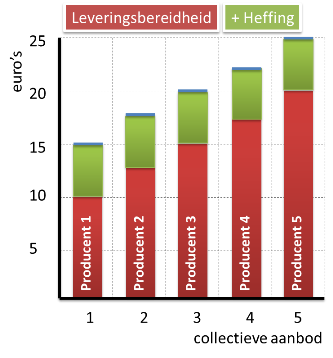
Wanneer de overheid nu de producenten belast met een accijns van € 5:
om nog steeds €10 over te houden, moet producent 1 € 15 aan de consumenten in rekening brengen. Er ontstaat nu een verschil tussen consumentenprijs (wat betaald moet worden) en producentenprijs (wat de producent overhoudt).
Producent 1 vraagt € 15 om zijn minimale € 10 over te houden
Producent 2 vraagt € 17,50 om zijn minimale € 12,50 over te houden
Producent 3 vraagt € 20 om zijn minimale € 15 over te houden
Producent 4 vraagt € 22,50 om zijn minimale € 17,50 over te houden
Producent 5 vraagt € 25 om zijn minimale € 20 over te houden
De aanbodlijn stijgt dus met het bedrag van de accijns!
Maar hoe pakken we dit aan met een aanbodvergelijking?
Stel een aanbodvergelijking van Qa = 2,5P – 15
Er komt een heffing van € 10
Stap 1 – verwissel Q en P van plek in de functie, zodat je bij elke hoeveelheid de minimale prijs (leveringsbereidheid) weet.
-2,5 P = -Q – 15
P = 0,4Q + 6
Stap 2 – tel de heffing op bij de prijs die de producent wil verdienen
P = (0,4Q + 6) + 10
P = 0,4Q + 16
Stap 3 – wissel P en Q van plek om er weer een aanbodfunctie van te maken
-0,4Q = -P + 16
Q’a = 2,5P – 40
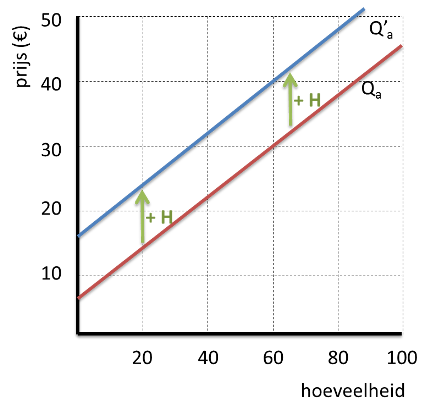
De aanbodlijn schuift dus naar boven. En wel met het bedrag van de accijns.
Maar dat wil niet zeggen dat de marktprijs óók met dit bedrag stijgt. De reactie van de consumenten (prijselasticiteit) op de wens van de producenten om méér te willen hebben zal bepalen hoeveel de prijs omhoog gaat.
Afwentelingspercentage
Het afwentelingspercentage geeft aan hoeveel procent van de heffing wordt afgewenteld op de consument.
| Elastische vraag Consumenten reageren relatief sterk op prijsveranderingen Qv = -6P + 240 |
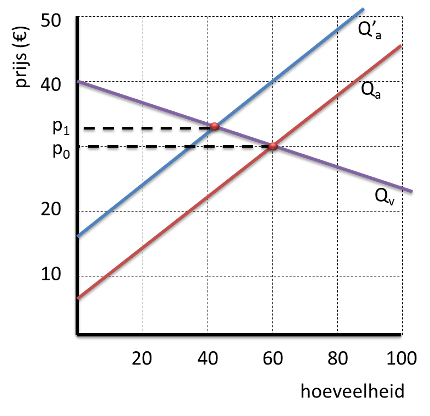
Doordat de consumenten veel minder gaan kopen, stijgt de prijs – ondanks de heffing – nauwelijks.
Qa = 2,5 P – 15
Q’a = 2,5P – 40 (na de heffing van €10)
Qv = -6P + 240
Oude evenwichtsprijs = € 30
Nieuwe evenwichtsprijs = € 32,94
Van de € 10 wordt dus uiteindelijk maar € 2,94 door de consumenten betaald.
Een afwentelingspercentage van
| Inelastische vraag Consumenten reageren relatief zwak op een prijsverandering Qv = -2P + 120 |
Doordat de consumenten nauwelijks minder gaan kopen, stijgt de prijs flink. Maar nog steeds minder dan de heffing.
Alleen wanneer de vraag volkomen inelastisch is (dus consumenten helemaal niet reageren op een prijsstijging), zal de heffing volledig kunnen worden doorberekend in de prijs.
Qa = 2,5 P – 15
Q’a = 2,5P – 40 (na de heffing van €10)
Qv = -2P + 120
Oude evenwichtsprijs = € 30
Nieuwe evenwichtsprijs = € 35,56
Van de € 10 wordt dus uiteindelijk € 5,56 door de consumenten betaald.
Een afwentelingspercentage van
Pas op:
Afwentelingspercentage is dus iets anders dan de procentuele stijging van de prijs!
Gevolgen van een heffing voor de welvaart
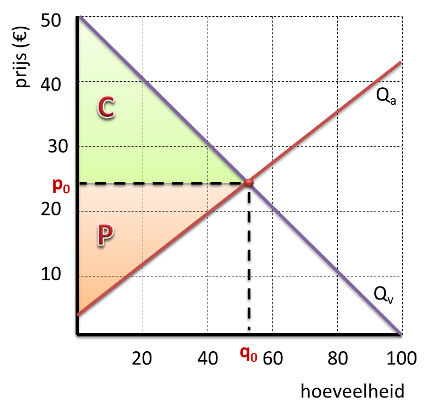
De bovenste afbeelding toont een markt van volkomen concurrentie.
Consumenten- en Producentensurplus – in de grafiek aangegeven met resp. een C en een P – zijn in deze situatie maximaal.
Er is sprake van een Pareto-efficiënte uitkomst.
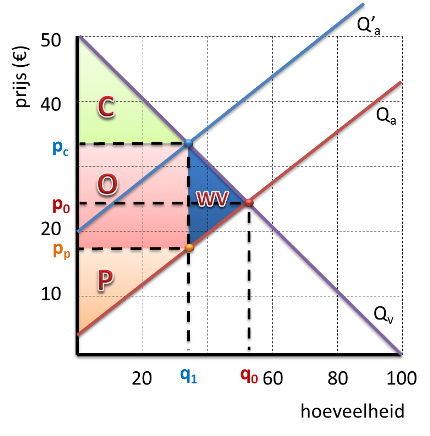
In de afbeelding daaronder heeft de overheid de producenten belast met een (flinke) heffing. Als gevolg daarvan is de aanbodlijn naar boven verschoven en ontstaat een nieuwe evenwichtsituatie, met een hogere prijs.
| Pc = | de consumentenprijs, waarin de heffing is verrekend. |
| Pp = | de producentenprijs, het bedrag dat de producenten overhouden nadat zij de heffing aan de overheid hebben betaald. |
| C | we zien dat het consumentensurplus ten opzichte van de uitgangssituatie flink is afgenomen. |
| P | we zien dat (ondanks de hogere consumentenprijs) ook het producentensurplus flink is afgenomen. |
| O | tegenover de afname van de welvaart die ontstaat door een kleiner consumenten- en producentensurplus, staat een bedrag dat de overheid ontvangt. Met dit bedrag kan de overheid o.a. collectieve goederen producen die weer welvaart opleveren. |
| WV | de toename van de welvaart (O) is kleiner dan het verlies aan welvaart. Per saldo daalt de welvaart met de driehoek WV. Deze Harberger-driehoek geeft het welvaartsverlies weer. Ook deze driehoek kun je natuurlijk uitrekenen met ½ × basis × hoogte
waarbij:
basis = bedrag van de heffing (pc – pp)
hoogte = afname productie (q0 – q1) |