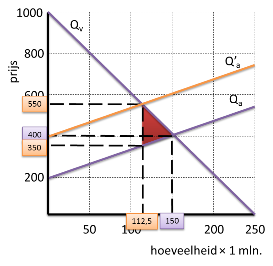
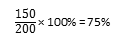Een markt van volkomen concurrentie kan beschreven worden met de volgende vergelijkingen:

Qv = -0,25P + 250
Qa = 0,75P – 150		 waarbij:
P= prijs in euro’s
Q = hoeveelheid in miljoen eenheden
a

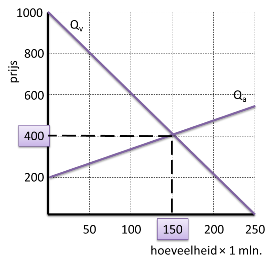
Teken de marktsituatie en geef de evenwichtsprijs aan.
b

Bereken de evenwichtsprijs en de evenwichtshoeveelheid.
c

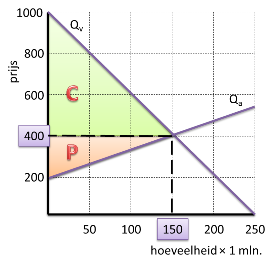
Arceer in de grafiek van vraag 1a het consumenten- en producentensurplus.
d

Bereken de omvang van het consumentensurplus.
e

Bereken de omvang van het producentensurplus.

Omdat met de productie van dit product veel milieuvervuiling ontstaat, legt de overheid de producenten een heffing van € 200 per product op.

f

Leg uit waarom door de heffing de aanbodlijn naar boven verschuift. Gebruik in je uitleg de term ‘leveringsbereidheid’.
g

Herleid de nieuwe aanbodfunctie.
h

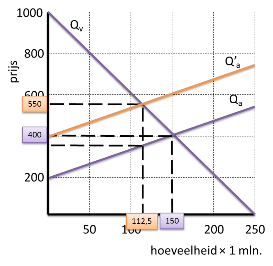
Teken de grafiek uit vraag 1a opnieuw en teken de nieuwe aabodfunctie erin.
i

Bereken hoeveel procent van de heffing op de consumenten wordt afgewenteld.
j

Bereken de omvang van de Harberger driehoek (het welvaartsverlies dat ontstaat door de heffing).

a
b Qa = Qv
0,75P – 150 = -0,25P + 250
P = 400 (euro’s)

Invullen in één van beide functies levert op: Q = 150 (miljoen eenheden)
 
c
d

Consumentensurplus:

½ × basis × hoogte =
½ × 150 mln × (1000-400) =
€ 45 mld.
e

Producentensurplus:

½ × basis × hoogte =
½ × 150 mln × (400-200) =
€ 15 mld.
f

De oude aanbodlijn geeft aan hoeveel bedrijven minimaal (per product) willen verdienen bij een bepaalde hoeveelheid producten. De lijn geeft hun leveringsbereidheid weer.
Nu bedrijven de overheid € 200 moeten betalen, zal het bedrag dat ze minimaal willen ontvangen met € 200 toenemen. Op die manier houden zij (netto) nog steeds hetzelfde bedrag over als voorheen.
g Stap 1 – verwissel Q en P van plek in de functie, zodat je bij elke hoeveelheid de minimale prijs (leveringsbereidheid) weet.

Qa = 0,75P – 150
-0,75P = -Q – 150
P = 1,33Q + 200
 
Stap 2 – tel de heffing erbij
P = (1,33Q + 200) + 200
 
Stap 3 – wissel P en Q weer van plek om er weer een aanbodfunctie van te maken
P = 1,33Q + 400
-1,33Q = -P + 400
Qa = 0,75P – 300
 
h Qa = Qv
0,75P – 300 = -0,25P + 250
P = 550 

Daaruit volgt: Q = 112,5 (mln)

 
i De consumenten betalen nu € 550. Vóór de heffing was dat € 400.
De heffing was € 200, waarvan de consumenten dus € 150 betalen.

Dat is dus
 
j De Harberger driehoek is in de grafiek weergegeven met de rode driehoek.

½ × basis × hoogte =
½ × (150 – 112,5) mln × 200 =
€ 3,75 mld.
print