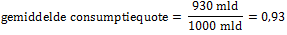Opgave 1

Een gesloten economie zonder overheid Waarbij:
(1)
(2)
(3)
(4)		 C =
I =
EV =
Y =		 0,9Y + 30
70
C + I
EV		 C =
I =
EV =
Y =		 consumptieve bestedingen
investeringen bedrijven
effectieve vraag
nationaal inkomen

 

1 Bereken de hoogte van het evenwichtsinkomen.
2 Wat is de betekenins van het begrip ‘evenwichtsinkomen’?
3 Bereken de voorraadmutatie indien er een nationaal inkomen van 800 wordt gerealiseerd. Geef aan of er sprake is van een toe- of een afname van de voorraden.
4 Hoe hoog zijn respectievelijk de gemiddelde en de marginale consumptiequote bij het evenwichtsinkomen?

Opgave 2

Een gesloten economie met overheid
 alle bedragen, tenzij anders vermeld in mld. euro’s
Waarbij:
(1) C = 0,75Yb + 40 C = consumptieve bestedingen
(2) Yb = Y – B Yb = besteedbaar inkomen
(3) B = 0,2Y B =
 belastingopbrengst
(4) I = 70 I =
 investeringen bedrijven
(5) O = 100 O = overheidsbestedingen
(6)
(7)		 EV =
Y =		 C + I + O
EV		 EV =
Y =		 effectieve vraag
nationaal inkomen
         
(8) Av = Av = werkgelegenheid (arbeidsvraag) (in arbeidsjaren)
(9) apt= 75.000 apt = arbeidsproductiviteit (in euro’s)
(10) Aa = 7,2 mln. Aa = beroepsbevolking (arbeidsaanbod) (in arbeidsjaren)
(11) U = Aa – Av U = werkloosheid (in arbeidsjaren)
5 Laat met een berekening zien dat de hoogte van het evenwichtsinkomen €525 mld. bedraagt.
6 Bereken de omvang van de werkloosheid bij het evenwichtsinkomen.
7 Wat is de waarde van de multiplier van de overheidsbestedingen.

De overheid wil de werkloosheid met 100.000 arbeidsjaren verminderen.

8 Bereken, m.b.v. de multiplier, met welk bedrag de overheid haar (autonome) bestedingen in dat geval moet verhogen.
9 Bereken de netto kosten van deze maatregel voor de overheid. Benoem in je antwoord ook expliciet het inverdieneffect.

Opgave 1

1 EV = C + I
EV = (0,9Y + 30) + 70
Y = 0,9Y + 30 + 70
1Y = 0,9Y + 100
1Y – 0,9Y = 100
0,1Y = 100
Y = 1000
 
2 We spreken van  ‘evenwichtsinkomen’  als de gerealiseerde productieomvang overeen komt met de omvang van de voorgenomen bestedingen.
 
3 C = 0,9·800 + 30 = 750
I  =                               70 +
EVex ante              = 820 (voorgenomen bestedingen)

Gezinnen zullen hun wensen (750 mld. consumeren) realiseren.
Omdat de totale productie 800 mld. en bedrijven voor 70 mld. wilden investeren, betekent het dat bedrijven 20 (mld) uit hun voorraden moeten halen (afname van de voorraad)
 
4 Gemiddelde consumptiequote:
Totale consumptie = 0,9·1000 + 30 = 930
Nationaal inkomen = 1000

Marginale consumptiequote:
c = 0,9
(Elke euro extra inkomen leidt tot 0,9 extra consumptie. Dat kun je aflezen in de consumptiefunctie.)

Opgave 2

5 EV = C + I + O

EV = (0,75Yb + 40) + 70 + 100
EV = 0,75Yb + 40 + 70 + 100
EV =0,75(Y – B) + 210
EV =0,75(Y – 0,2Y) + 210
EV =0,75·0,8Y + 210
EV = 0,6Y + 210

Y = 0,6Y + 210
0,4Y = 210
Y = 525
 
6 Av
Bij een totale productie van 525 mld.
En een productie van 75.000 per arbeidsjaar.
Zijn er 7 mln. arbeidsjaren nodig ( = werkgelegenheid)

Aa
De beroepsbevolking bedraagt 7,2 mln. arbeidsjaren.

U
Er heerst dus 200.000 arbeidsjaren werkloosheid.

 
7 Wanneer we in voor model een eindvergelijking opstellen, luidt die 

Deze vermenigvuldigingsfactor geldt voor alle autonome bestedingen, dus ook voor Oo, en heeft de waarde  2,5.
 
8 Als de werkloosheid met 100.000 moet afnemen.
En de productie per arbeidsjaar bedraagt 75.000.
Dan moet de totale productie met 7,5 mld. toenemen.

De multiplier van de (autonome) overheidsbestedingen bedraagt 2,5 (vraag 7)

ΔY = 2,5 • ΔOo
7,5 = 2,5 • ΔOo
ΔOo = 3

Dus de autonome overheidsbestedingen moeten met 3 mld. toenemen.
 
9 De overheid geeft dus 3 mld. extra uit.

Het nationaal inkomen stijgt hierdoor met 7,5 mld.
De belastingfunctie luidt: B = 0,2Y
Dankzij 7,5 mld. extra inkomen, krijgt de overheid 1,5 mld. extra belastinggeld binnen (inverdieneffect)

De netto kosten van deze maatregel bedragen dus: (3 – 1,5 =) 1,5 mld
print