Differentiëren wordt gebruikt om de helling van een lijn te berekenen.
Je berekent in zo’n geval dus de toe- of afname van een bepaalde grootheid (als je een heel klein stukje opschuift op de lijn).
Differentiëren wordt in de vwo-stof van het vak economie een paar keer gebruikt.
De uitleg hierover is in twee onderdelen gesplitst:
- Een algemene inleiding over differentiëren:
uitleg over wat je nu eigenlijk doet met differentiëren en uitleg van de standaardregel (uit de wiskunde) - Een kort overzicht van de toepassingen bij economie.
Inleiding differentiëren
externe uitleg differentiëren
Formule differentiëren:
| In de originele formule staat | De eerste afgeleide van die factor is dan: |
| y = a · xn | 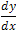 = a · n · x n-1 = a · n · x n-1 |
Bij het vak wiskunde wordt daarvoor vaak gewoon y’ opgeschreven als er wordt gedifferentieerd.
Met de omschrijving 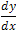
Deze lastige notatiewijze lijkt overbodig, maar zodra een vergelijking meerdere onbekenden heeft is het absoluut noodzakelijk.
Dus:
| In de originele formule staat | De eerste afgeleide van die factor is dan: | |
| y = a · xn | 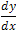 = a · n · x n-1 = a · n · x n-1 |
|
| 5 x3 | 5·3 x3-1 | 15x2 |
| 3 x2 | 3·2 x2-1 | 6x |
| 15 x | 15·1 x1-1 | 15 |
| 15 | y blijft contant (15) | 0 |
| 5x3 – 12x + 5 | 5·3 x3-1 – 12·1 x1-1 +constante | 15x2 – 12 |
Toepassingen bij economie
Onderstaande toepassingen worden verder uitgelegd bij het domein Markten.
