§ 1.4 Produceren bij onvolkomen concurrentie CV

Q_v = -25P + 750
P = -0,04Q + 30
TO = -0,04Q² + 30Q
MO = -0,08Q + 30

Q_v = -20P + 1.000
P = -0,05Q + 50
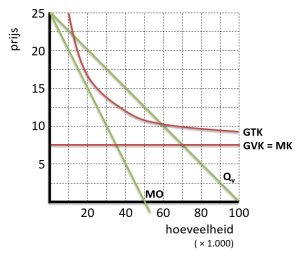
TO = -0,05Q² + 50Q
MO = -0,1Q + 50

Maximale omzet haalt een monopolist bij een productie waar geldt: MO=0

MO = -0,1Q + 50
0 = -0,1Q + 50
Q = 500 ⇒ bij een productie van 500 stuks

b

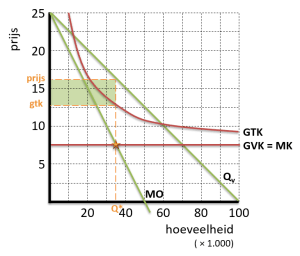
Maximale winst haalt de monopolist bij een productie waar geldt: MO = MK

Q_v = -4P + 100
P = -0,25Q + 25
TO = -0,25Q² + 25Q
MO = -0,5Q + 25

MK = 7,5

MO = MK
-0,5Q + 25 = 7,5
Q = 35 (productie waarbij maximale winst wordt gehaald)

P = -0,25Q + 25
P = -0,25×35 + 25
P = 16,25

c

d

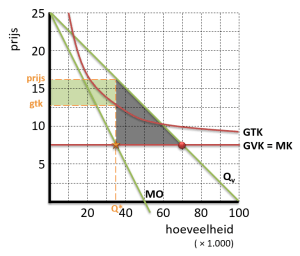
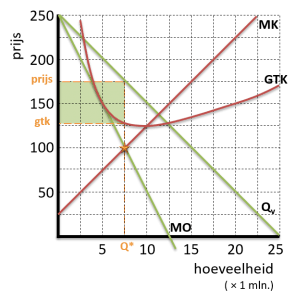
Bij volkomen concurrentie zou de producent moeten leveren tegen zijn minimale leveringsbereidheid (MK).
Daardoor zou de markt in evenwicht komen in de rode punt.

De monopolist kiest echter de prijs die hoort bij zijn streven naar maximale winst (oranje ster).

De zwarte driehoek is het welvaartsverlies dat ontstaat door het monopolie.

Hoogte driehoek = € 16,25 – € 7,50
Breedte driehoek = 70 – 35 = 35 (000 stuks)

Welvaartsverlies = ½ × 35.000 × € 8,75 = € 153.125

MK = 10Q + 25
MK = TVK’

TVK = 5Q² + 25Q

GVK = TVK/Q
GVK = 5Q + 25

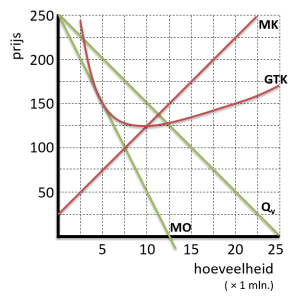
Een monopolist haalt maximale winst bij de productie waar geldt: MO = MK

Q_v = -0,1P + 25
P = -10Q + 250
TO = -10Q²+ 250Q
MO = -20Q + 250

MK = 10Q + 25

MO = MK
-20Q + 250 = 10Q + 25
Q = 7,5 (mln. eenheden)

P = -10Q + 250
P = -10×7,5 + 250
P = 175 (euro)

Maximale winst wordt gehaald bij:
Q = 7,5 (mln. eenheden)
P = 175 (euro)

De kosten zijn dan:
GTK = 5Q + 25 + (500/Q)
GTK = 129,17

De winst bedraagt:
(€ 175 – € 129,17) × 7,5 mln. stuks ≈ € 343,7 mln.